В кубе сколько квадратов доски: Сколько досок 6 метров в кубе? (таблица, формула, пример расчёта) – "Строим Дом"

Содержание

Сколько в кубе половой доски

Рассматриваемый материал задействуется в домах, квартирах. Преимуществами данного пиломатериала являются натуральность, экологичность, простота установки, длительность эксплуатации. Людям, которые планируют сделать ремонт, необходимо знать, сколько в кубе половой доски.

Виды

Перед тем, как перейти к определению того, сколько половых досок в кубе, надо предварительно выяснить, какие виды материала бывают. Перед покупкой следует узнать, сколько стоит 1 м2 половой доски на нашем сайте. Для этого вы можете воспользоваться нашим прайс-листом https://ruslesgroup.ru/price-list/. Важно обратить внимание, что количество единиц вычисляется по одному и тому же принципу. Разновидность пиломатериала не играет роли в процессе вычисления.

Разновидности:

Половая доска из лиственницы .
Шпунтованная.
Евро.
Сосновая.

Куб доски половой: пример расчета

Стоимость куба половой доски у нас можно рассчитать самостоятельно. Выбирая сырье для укладки на лаги, нужно обращать внимание на самый важный критерий – толщину ламелей. Материал выпускается разной толщины: 20, 28 и 35 мм.

Толщина материала, мм	Расстояние между лагами, см	Покрываемая площадь пола одним кубометром доски, м²
20	30	50
28	40
35	60	28,5

Толщина материала, мм

Расстояние между лагами, см

Покрываемая площадь пола одним кубометром доски, м²

28,5

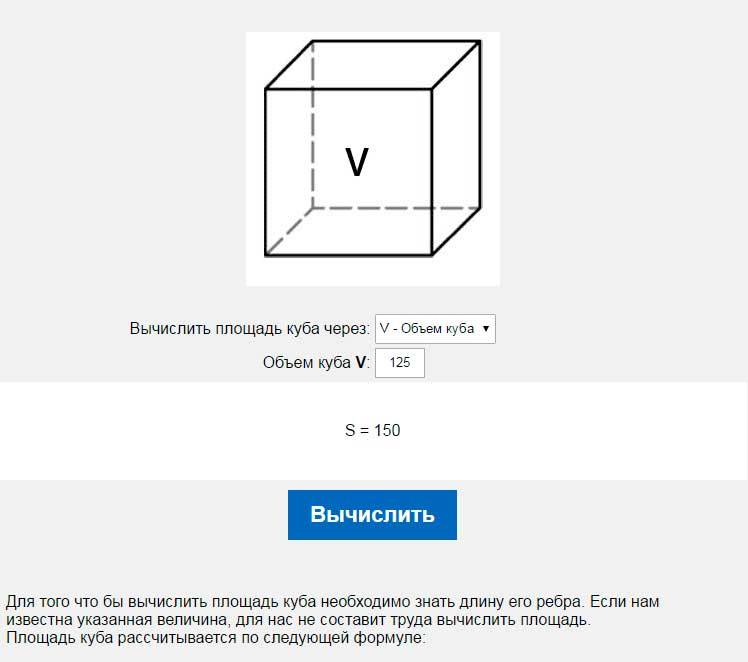
Подсчет производится исходя из понятной формулы. Объем равняется произведению длин трех сторон.

Символьная формула:

1 / (L*h*b) = N, где

h, b, L – высота, ширина, длина в метрах;

N – количество в 1 м³, штук.

Не нужно забывать, что подсчет по данной формуле носит приблизительный характер. Число может получиться дробное. Во время приобретения можно забрать объем пиломатериала, который является кратным целому и округленным в большую сторону.

Наша компания предлагает клиентам такой материал, как половая доска цена за 1 куб которой доступна каждому человеку. Всегда следует покупать больше, чем необходимо. Это объясняется тем, что во время ремонта может быть использовано больше пиломатериала. Демократичная цена куба половой доски в нашем интернет-магазине позволяет запастись данным строительным материалом.

Сколько стоит куб половых досок?

Для того чтобы узнать, сколько квадратных метров способен покрыть один кубический метр материала, следует округленное число досок в кубе умножить на площадь одной единицы (произведение длины на ширину). Рассчитать можно по такой формуле:

S = N * b * L, где

S – площадь в м², “зашиваемая” 1 м³ сырья.

В основном все расчеты половой доски производятся в квадратных метрах. Для удобства вычислений вы можете воспользоваться нашим калькулятором половой доски https://ruslesgroup.ru/calculator/

Расчитываем объем и количество метров доски 40х150х6000 в кубе.

Общепризнанной мерой измерения древесных материалов является кубометр. Большая часть всей продукции распиловки – обрезные, не обрезные, строганные и другие древесные материалы измеряется в метрах кубических. Другими словами 1 м³ – это объем равный 1м в длину, ширину и толщину.

Сколько кубов в одной доске 40х150х6000

Расчет кубатуры древесины зависит от 2-х ее характеристик, а в частности от того обработана она или нет.

Чтобы узнать, сколько кубов в одной доске 40х150х6000 (обрезной) следует использовать таблицу расчетов или такую формулу:

V=a × b × l, где

a – высота;
b – ширина;
l – длина.

Объем высчитывается в кубометрах, поэтому все величины следует предварительно перевести метры из миллиметров. Соответственно толщина данного материала составляет – 0, 04 м, ширина 0,15 м, а длина 0,6 м. Следующим шагом будет непосредственно расчет кубатуры:

V=0,04 × 0,15 × 6 = 0,036

Соответственно в одной обрезной 6-метровой «сороковке» – 0,036 м³.

Для не обрезных нет точных табличных данных. Средняя кубатура деревянного элемента с сечением 40 х 6000 – 0,05 м³.

Сколько досок в кубе

Пиломатериал обрезной 40 × 150 × 6000 широко используется в строительстве и мебельном производстве, для изготовления тары, в оформлении интерьеров и других целей. Чтобы узнать, сколько штук «сороковок» в кубе необходимо узнать кубатуру 1-й доски. Дальнейший расчет не представляет особой сложности, достаточно лишь воспользоваться специальным калькулятором или такой формулой:

K=1 м³/Вд, где Вд – м³ дощечки.

В нашем случае расчет будет выглядеть таким образом:

K=1/0,036 = 27,777 шт.

Соответственно в 1 кубометре пиломатериалов с сечением 40 × 150 × 6000 будет приблизительно 28 шт. Лучше округлять в большую сторону.

Сколько метров в кубе

В 1 кубометре пиломатериалов может быть разное количество квадратных метров. Зависит этот показатель от толщины изделия. Поэтому, чтобы узнать, сколько метров в одном кубе дерева необходимо разделить 1 м3 на толщину.

T=1/ а, где:

В нашем примере толщина пиломатериала 40 мм, что соответственно составляет 0,04 м. подставляем в формулу и получаем:

T=1/ 0,04 = 25 м²

В итоге в 1 кубометре доски толщиной 4 сантиметра будет равен 25 м².

Кубатура одной доски обрезной толщиной 40 мм

Кубический объем пиломатериала обрезного 40 х 150 х 6000, а также количество досок и квадратных метров 1 кубометре, можно увидеть в таблице. Она поможет правильно определить необходимый объем строительных материалов, чтобы не понести лишних расходов при их приобретении.

Ширина и длина (мм)	Сколько м²в 1 доске	Количество (шт) в 1 м³	Сколько метров в 1 м³
150 × 6000	0,036	27	25

Сколько квадратных метров доски в кубе? | DZEN BLOGGER.

Сколько квадратных метров доски в кубе: габариты изделий, количество деталей, расчет объема и площади?

Сколько квадратных метров доски в кубе: габариты изделий, количество деталей, расчет объема и площади

Все фото из статьи

Сколько квадратных метров доски в кубе?Сколько квадратных метров доски в кубе?Сколько квадратных метров доски в кубе?Сколько квадратных метров доски в кубе?Сколько квадратных метров доски в кубе?Сколько квадратных метров доски в кубе?Сколько квадратных метров доски в кубе?Сколько квадратных метров доски в кубе?Сколько квадратных метров доски в кубе?

Содержание

Разбираться, сколько досок в квадратном метре, сколько кубов материала нужно для реализации того или иного проекта, сколько квадратов можно обшить одним кубометром материала и т. д., должен любой, кто планирует стройку или ремонт. И хоть сегодня несложно найти табличные значения практически для любой ситуации, желательно все же понимать, как осуществляются расчеты, и при необходимости уметь провести вычисления своими руками.

Сколько квадратных метров доски в кубе?

Чтобы понять, сколько здесь материала, придется провести нехитрые расчеты

Габариты досок

Кубометр доски — это сколько? Один из самых распространённых вопросов, которые задают мастера-новички. На самом деле на этот вопрос можно дать предельно простой ответ: это, смотря о каком пиломатериале речь!

Сколько квадратных метров доски в кубе?

Схема определения линейного размера пиломатериала

Как правило, для строительных и ремонтных работ применяют заготовки, произведенные по ГОСТ 8486-86. Этот норматив, регламентирующий основные требования к пиломатериалам хвойных пород (для лиственных есть отдельный документ — ГОСТ 2695-83), определяет, какой размер может иметь изделие.

В принципе, подобрать нужную деталь несложно, но все же есть определенные ограничения, которые и лимитируют производство заготовок:

толщина – от 16 до 75 мм;
ширина – от 75 до 275 мм;
длина — от 1 до 6 м.

Естественно, встречаются и отступления. Так, при необходимости можно заказать изготовление деталей с другим соотношением толщины и ширины. Их цена, конечно, будет выше, чем стандартных, но при необходимости и наличии подходящего сырья можно выпилить практически любую заготовку.

Сколько квадратных метров доски в кубе?

Стандартная длина составляет от 1 до 6 м

Что касается длины, то здесь все несколько сложнее. Найти заготовки длиннее 6 м получается далеко не всегда, поскольку эта величина ограничена габаритами товарного вагона. Так что более длинные доски пилятся исключительно под заказ и перевозятся автотранспортом, что удорожает материал.

В принципе, этой информации будет вполне достаточно, чтобы мы, зная основные параметры изделий, могли рассчитать, сколько 6 метровых досок в кубе, и какую площадь они займут при обшивке либо укладке на пол.

Примеры расчетов

Количество деталей в кубе

Сколько квадратных метров доски в кубе?

Пиломатериалы обычно реализуются по объему

Итак, первую часть этого раздела мы посвятим определению того, сколько досок в кубометре. Задача эта достаточно проста, поскольку нам достаточно 1 м3 поделить на объем одной детали.

Единичный объём вычисляем по формуле Д х Ш х Т, где:

Д – длина;
Ш – ширина;
Т – толщина.

Обратите внимание!

Рассчитывая, сколько досок в одном кубометре, нужно не забывать о переводе единиц, так как обычно параметры поперечного сечения указываются в миллиметрах, а длина – в метрах.

Сколько квадратных метров доски в кубе?

Фото калькулятора, используемого для вычислений

В качестве примера вычислим, сколько в кубе 4 метровых досок шириной 150 мм и толщиной 25 мм:

Вычисляем объем одной заготовки: 4 х 0,150 х 0,025 = 0,015 м3.
Определяем количество деталей: 1 / 0,015 = 66,7.
Округляем до целого значения, получая 66 штук.

Обратите внимание!

Обычно округляют до последней целой цифры.

Это, конечно, несколько противоречит правилам математики, но в данном случае стоит ориентироваться на сложившуюся практику.

Чтобы вам было проще рассчитывать количество досок в кубе — таблица 4 метра / 6 метров приводится ниже:

Длина, м

Толщина, мм

Ширина, мм

Объем единицы, м3

Количество, штук

100

0, 016

150

0,024

100

0,020

150

0,030

100

0,024

150

0,036

100

0,030

150

0,045

Естественно, имея под рукой такую таблицу, посчитать, сколько метров доски в кубе (погонных, о квадратных мы поговорим ниже), будет очень легко: берем количество досок и умножаем на их длину.

Так, для деталей 4000х50х100 этот показатель будет равен: 50 х 4 = 200 м. пог.

Сколько квадратных метров доски в кубе?

Еще один вариант таблицы соотношения объема и количества

Объем и площадь

Следующая инструкция посвящена определению площади, которую можно обшить/покрыть, израсходовав одни кубометр пиломатериала.

Сколько квадратных метров доски в кубе?

Чтобы обустроить напольное покрытие, как на этом фото, нужно заранее вычислить объем материала для отделки требуемой площади

Здесь в первую очередь необходимо определить площадь одного элемента, просто умножив его длину на ширину. Так, если мы планируем обшивать стену деревянной вагонкой 3 м с шириной 220 мм и толщиной 20 мм, то площадь одной доски будет равна 3 х 0,22 = 0,66 м2.
Затем определяем количество таких изделий в кубометре. Объем одной доски будет равен 3 х 0,22 х 0, 02 = 0,0132 м3. Следовательно, в кубе у нас будет 1 / 0,0132 = 75 деталей заданного размера.
Далее полученное количество умножаем на площадь одной доски: 75 х 0,66 = 49,5 м2.

Обратите внимание!

Высчитывая, сколько квадратных метров в 1 кубе доски – вагонки, нужно принимать во внимание не фактические размеры панелей, а размеры «видимой части».

Связано это с тем, что при монтаже шипы замковых элементов скрываются в пазах, и ширина уменьшается, так что расхождение теоретического расчета с фактическим может доходить до 8 -10%.

Сколько квадратных метров доски в кубе?

При расчетах с вагонкой длина шипа не учитывается

Также при переводе кубатуры в объем нужно помнить, что иногда возникает необходимость укладки досок без стыков. При этом следует подбирать детали с такой длиной, которая обеспечит появление минимального количества отходов, иначе наши затраты на покупку материала существенно (и неоправданно!) возрастут.

Советы при работе с необрезными деталями

Все рекомендации, приведенные выше, касались работы с обрезной доской, ровным деревянным брусом, вагонкой и т.д. Однако для решения различных задач иногда задействуются необрезная доска и горбыль, которые имеют неправильную форму.

В этом случае для вычисления хотя бы приблизительного объема материала поступаем следующим образом:

Сколько квадратных метров доски в кубе?

Объем необрезной заготовки или горбыля вычислить куда сложнее

Сначала определяем среднюю толщину заготовки. Для этого выполняем несколько промеров в самой толстой и самой тонкой части, суммируем полученные результаты и делим на количество измерений.
Затем рассчитываем среднюю ширину по тому же алгоритму.

Обратите внимание!

Чем ближе форма изделия к правильному параллелепипеду, тем меньше промеров нужно сделать для получения сколько-нибудь точного значения.

Полученные средние величины перемножаем, затем умножаем на длину необрезной планки/горбыля, и получаем объем единицы пиломатериала.

Можно поступить и несколько проще. Зная, что выход полноценной доски из необрезных заготовок составляет около 70 – 80% по объему, мы просто приобретаем сырье с запасом, умножая требуемую величину на коэффициент 1,25 — 1,3. Впрочем, так мы тоже получим только приблизительный результат, потому вероятность избытка/недостатка материала все же будет присутствовать.

Заключение

Мы надеемся, что следуя приведенным советам, вы разберетесь, как посчитать квадратный метр доски, как определить количество деталей в кубометре и т.д. Более подробную информацию можно найти на видео в этой статье, а если у вас в ходе изучения методик возникнут вопросы, вы сможете задать их в комментариях ниже!

https://rubankom. com/materialy/pilomaterialy/doski/1583-skolko-kvadratnyh-metrov-doski-v-kube

Сколько досок в 1 кубе пиломатериала, сколько штук в кубе – таблица и пример расчета

Для того чтобы посчитать, какое количество досок той или иной конфигурации содержится в одном кубическом метре, на нашем сайте доступна простая таблица расчетов. Воспользовавшись ею, вы сможете узнать, какое количество пиломатериалов понадобится вам для тех или иных нужд.

Итак, рассмотрим на примере обрезной доски размером 30х150х4000 мм:

1. Рассчитываем объем одной доски в м³

0,03 м · 0,15 м · 4 м = 0,018 м³

2. Рассчитываем количество досок в штуках на каждый кубический метр

1 м3 / 0,018 м³ = 55 шт./м³

3. Расчет метров квадратных в кубометре пиломатериала

1 м³ / 0,03 м = 33 м²/м³

Аналогичным образом можно производить расчет досок любой конфигурации, просто подставляя в формулу определенные значения.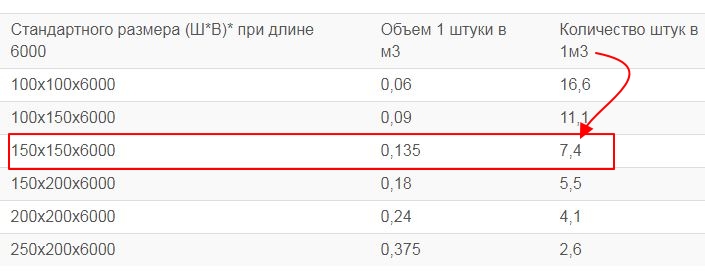 Эта формула будет полезна в случае, если вы желаете посчитать необходимое количество досок, нужное для вашего проекта.

Хотите перекрыть пол или определяетесь с количеством досок для перекрытия крыши? Мы поможем вам рассчитать нужный объем, руководствуясь простыми расчетами, представленными на этой странице.

Таблица расчета шт. досок в кубе

№	Размер	Объём доски (м³)	Штук в 1 м³	Штук в 1 м²
1	Доска 20х100х6000 мм	0,012 м³	83 шт.	50 м2
2	Доска 20х120х6000 мм	0,0144 м³	69 шт.	50 м2
3	Доска 20х150х6000 мм	0,018 м³	55 шт.	50 м2
4	Доска 20х180х6000 мм	0,0216 м³	46 шт.	50 м2
5	Доска 20х200х6000 мм	0,024 м³	41 шт.	50 м2
6	Доска 20х250х6000 мм	0,03 м³	33 шт.	50 м2
7	Доска 25х100х6000 мм	0,015 м³	67 шт.	40 м2
8	Доска 25х120х6000 мм	0,018 м³	55 шт.	40 м2
9	Доска 25х150х6000 мм	0,0225 м³	44 шт.	40 м2
10	Доска 25х180х6000 мм	0,027 м³	37 шт.	40 м2
11	Доска 25х200х6000 мм	0,03 м³	33 шт.	40 м2
12	Доска 25х250х6000 мм	0,0375 м³	26 шт.	40 м2
13	Доска 30х100х6000 мм	0,018 м³	55 шт.	33 м2
14	Доска 30х120х6000 мм	0,0216 м³	46 шт.	33 м2
15	Доска 30х150х6000 мм	0,027 м³	37 шт.	33 м2
16	Доска 30х180х6000 мм	0,0324 м³	30 шт.	33 м2
17	Доска 30х200х6000 мм	0,036 м³	27 шт.	33 м2
18	Доска 30х250х6000 мм	0,045 м³	22 шт.	33 м2
19	Доска 32х100х6000 мм	0,0192 м³	52 шт.	31 м2
20	Доска 32х120х6000 мм	0,023 м³	43 шт.	31 м2
21	Доска 32х150х6000 мм	0,0288 м³	34 шт.	31 м2
22	Доска 32х180х6000 мм	0,0346 м³	28 шт.	31 м2
23	Доска 32х200х6000 мм	0,0384 м³	26 шт.	31 м2
24	Доска 32х250х6000 мм	0,048 м³	20 шт.	31 м2
25	Доска 40х100х6000 мм	0,024 м³	41 шт.	25 м2
26	Доска 40х120х6000 мм	0,0288 м³	34 шт.	25 м2
27	Доска 40х150х6000 мм	0,036 м³	27 шт.	25 м2
28	Доска 40х180х6000 мм	0,0432 м³	23 шт.	25 м2
29	Доска 40х200х6000 мм	0,048 м³	20 шт.	25 м2
30	Доска 40х250х6000 мм	0,06 м³	16 шт.	25 м2
31	Доска 50х100х6000 мм	0,03 м³	33 шт.	20 м2
32	Доска 50х120х6000 мм	0,036 м³	27 шт.	20 м2
33	Доска 50х150х6000 мм	0,045 м³	22 шт.	20 м2
34	Доска 50х180х6000 мм	0,054 м³	18 шт.	20 м2
35	Доска 50х200х6000 мм	0,06 м³	16 шт.	20 м2
36	Доска 50х250х6000 мм	0,075 м³	13 шт.	20 м2

инструкция, фото- и видео-уроки, цена

Если вы задумали сделать ремонт или приступили к строительству загородного дома, то вполне вероятно, что у вас возникнет необходимость в приобретении пиломатериала. При осуществлении такой покупки очень часто встает вопрос о том, какое количестве досок соответствует одному кубическому метру пиломатериала, или какую площадь поверхности можно облицевать одним кубометром.

Панели из дерева для внутренних работ.

КОЛИЧЕСТВО ЕДИНИЦ В КУБИЧЕСКОМ МЕТРЕ.

Для наглядности выполним расчёт и определим, сколько штук обрезной доски (габариты 150х25х6000 в миллиметрах или 0,15х0,025х6 в метрах) находится в одном кубометре.

Находим объём одной доски: 0,15х0,025х6 = 0,0225 м3
Определяем количество досок в одном кубическом метре и округляем до целого числа (именно так идет подсчет в торговой сети): 1:0,0225 = 44,44 шт.=44 шт.

КОЛИЧЕСТВО КВАДРАТОВ В КУБОМЕТРЕ

Чтобы выполнить отделку стен каким-либо облицовочным материалом, необходимо узнать какую площадь можно облицевать из одного кубического метра при определенной толщине этого материала.

Вид после облицовки вагонкой

Расчёт выполняется в следующей последовательности:

Определяемся с необходимой толщиной обрезной доски. Для примера принимаем 0,025 м (25 мм).
Рассчитываем площадь, которую можно облицевать одним кубическим метром материала: 1 : 0,025 = 40 м2.
Делаем замеры и считаем площадь стены. Например, стена 4х2,5 м имеет площадь 10 м2.
Определяем необходимый объём досок для покупки: 10:40=0,25 м3.
Из предыдущего примера мы знаем, что объём одной доски составляет 0,0225 м3.
Определяем необходимое количество досок: 0,25:0,0225=11,11шт.
Покупаем с запасом 12 штук, общим объёмом: 0,0225х12=0,27 м3.

Вывод: Придерживаясь этого алгоритма расчета можно, подставляя свои значения, найти необходимый для облицовки объём пиломатериала.

РАСЧЁТ МАТЕРИАЛА ДЛЯ ОТДЕЛКИ

Материалы для облицовки стен нашли широкое применение, как для внутренних, так и для наружных отделочных работ. Их особенностью является простота монтажа, минимум подготовительных работ и большие межремонтные сроки эксплуатации.

Монтаж в вертикальном направлении

ВО ВНУТРЕННЕМ ПРОСТРАНСТВЕ

Для расчета материала необходимо выполнить ряд операций:

Составить список помещений, в которых планируются отделочные работы.
В каждом помещении определиться, что подлежит отделке (стены, пол, потолок).
Рисуем и нумеруем планы (прямоугольники), куда в дальнейшем будем наносить размеры:

План пола;
План потолка;
План каждой стены подлежащей отделке. Если на стене имеются окно или дверь, то эти проёмы наносим на план.

Измеряем и записываем полученные размеры (в метрах, с точностью до второго знака после запятой) в ранее заготовленные планы:

Для пола замеряем длину и ширину помещения. Замеры делать от стен, а не от плинтуса. Эти размеры проставить и на план потолка.
Для каждой стены замеряем её длину и высоту. Если есть дверь, то измеряем её высоту и ширину, а также замеряем размер от двери до любой примыкающей стены. Также поступаем и с оконным проёмом, но дополнительно измеряем расстояние от пола до низа окна.

Подсчитываем площади стен, пола, потолка по каждому помещению. Площади окон и дверей вычитаем из площади стен.
Суммируем полученные результаты. Как правило, к общей сумме добавляется десять процентов на непредвиденные обстоятельства.

НА ФАСАДЕ СТРОЕНИЯ

Для наружных и внутренних облицовочных работ порядок выполнения замеров и подсчета площадей не имеет принципиальных отличий. Площадь чердачного фронтона имеющая, как правило, форму близкую к треугольнику будем считать в запас, как площадь треугольника (умножаем длину на высоту и делим на два).

Фото 4. Фасад здания после окончания отделочных работ

Порядок операций при выполнении замеров и подсчета площадей для наружных облицовочных работ:

Схематично рисуем планы фасадов с нанесением оконных и дверных проёмов. (Не забываем нанести чердачный фронтон и входную группу).
Измеряем и записываем полученные размеры в заготовленные планы.
Выполняем подсчет площадей по каждому фасаду.
Из общей площади вычитаем площадь оконных и дверных проёмов.

ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ

Чтобы определить объём облицовочного материала, необходимо расчётную площадь фасада, за вычетом оконных и дверных проёмов, умножить на толщину отделочного материала. Единица измерения метр.
Для определения облицовочного материала в штуках необходимо расчётную площадь фасада разделить на площадь одной доски.
Определяя площадь доски при соединении досок способом «паз-шип», необходимо из размера доски по ширине исключить выступающую часть шипа.

Различные размеры у пиломатериалов

МАССА ТОВАРА В ЗАВИСИМОСТИ ОТ ФАКТОРОВ

Чтобы определиться с массой отделочного материала, необходимо знать его объёмный вес. Объёмный вес облицовочного материала из древесины зависит от таких факторов при изготовлении, как порода древесины и её влажность. В таблице 1 даны сравнительные показатели объемного веса в кг/м3, в зависимости от породы и влажности древесины.

Древесина Влажность	Бук, граб, дуб	Лиственница	Сосна, ольха	Кедр, липа, ель
10-18%	700	600	500	450
19-23%	750	650	550	500
24-45%	800	700	600	550
Более 45%	1000	900	800	800

В ЗАКЛЮЧЕНИЕ

Шесть шагов для определения объёма облицовочных материалов:

Выполнить замеры.
Посчитать площади подлежащие облицовке.
Сходить в магазин и определить понравившуюся марку товара и записать основные размеры доски (длину, ширину, толщину), а также стоимость.
В зависимости от расчётной площади и толщины доски определить объём облицовочного материала, который необходимо приобрести. Полученные значения увеличиваем на 10%.
Для контроля при покупке определяем, какое количество досок будет соответствовать объёму закупаемого материала, рассчитанному в кубических метрах.
Определяем общую стоимость материала и идем покупать.

Примечание

При покупке необходимо оценить качество товара и его внешний вид.

Особое внимание обратить на возможное отклонение от геометрических размеров и прямолинейности. Материал с обнаруженными дефектами нужно заменить.

Сколько досок в кубе: расчет количества и примеры

Куб досок, а это сколько? Вопрос, с которым рано или поздно сталкивается любой строитель или человек, составляющий смету расходов на строительство полностью или частично деревянного объекта. Для того, чтобы правильно рассчитать количество нужных материалов, расходы, а также спланировать строительство, нужно четко понимать, сколько древесины необходимо.

Из этого также вытекает два обстоятельства: нужно знать стандарты подсчета кубатуры древесины и пиломатериалов, а также особенности измерений и расчетов, которыми руководствуются как продавцы сырья, так и профессиональные строители.

Кубический метр

Кубический метр — это объем, который соответствует кубу с размерами 1 м * 1 м * 1 м.

При измерении и расчете количества пиломатериалов, которые обычно имеют большую длину и маленькое сечение (ширину и толщину), как правило, не проводят вычисление для большого количества материала. Обычно достаточно измерения одного элемента, знания стандартных размеров, а также правил расчета общего количества в одном кубе.

Проще это понять на примере:

Нужен пиломатериал толщиной 25 мм, шириной 150 мм и длиной 4 метра. Посчитаем, сколько штук будет входить в один куб. Для этого все размеры переводятся в метры:

толщина — 25 мм = 0,025 м;
ширина — 150 мм = 0,15 м;
длина — 4 м.

Объем данной составляет 0,025 м умножить на 0,15 м и умножить на 4 м, что равняется:

V = 25 мм * 150 мм * 4 м = 0,025 м * 0,15 м * 4 м = 0,015 м³.

Таким образом легко увидеть, что одна — это 0,015 куба или, переводя в количество, можно узнать, сколько досок в 1 кубе.

Расчет количества досок в одном кубе: 1 м³ / 0,015 м³ = 66⅔.

Согласно стандартам, дробная часть при расчете количества не учитывается, поэтому количество указывается как 66 ровно.

Определим также, сколько квадратных метров площади будет в 1 кубе, разделив объем куба на толщину:

1 м³ / 0,025 = 40 м²/м³;

Итак, формулы расчета на данном примере:

Объем: 0,025 м * 0,15 м * 4 м = 0,015 м³;

Количество досок в кубе в штуках: 1 м³ / 0,015 м³ = 66 шт./м³;

Площадь пиломатериалов, входящих в кубический метр, в квадратах: 1 м³ / 0,025 м = 40 м²/м³

Такой простой расчет количества досок в одном кубе для размеров 25 * 150 * 4000 мм подойдет и для других параметров, например для той же ширины 150 мм, толщины 25 мм и длины 6 м. Он помогает избежать путаницы или обмана, когда производитель пиломатериалов или перевозчик рассчитывают на невнимательность заказчика, и таких случаев много.

Стоит понимать, что обычно расчет количества досок в одном кубе проводится не так легко и часто зависит от типа пиломатериала или характера его складирования. Кроме того, при заказе и расчете с поставщиком заказчик древесины часто может переплатить, если не обратит внимание на то, что сумма округлена к большему числу.

Есть еще одна маленькая хитрость, которую могут использовать недобросовестные продавцы. Дело в том, что доска обрезная стандартной длины 6 метров — не 6-метровая, и на самом деле ее длина составляет 6,1 или 6,2 метра. 6 — это не только номинальная величина, именно ее продавцы должны использовать в расчетах, но некоторым из них это не мешает, и таким образом они увеличивают номинальный объем на несколько процентов, что делает покупку более затратной.

Виды материалов

Один кубический метр древесины в расчете на количество для разных видов материалов будет отличаться. Когда говориться об идеально ровных брусьях и обрезных досках, то их можно сложить в достаточно плотную стопку которая полностью будет заполнена древесиной. На практике приходится иметь дело не только с брусьями или обрезной, но и с более сложным пиломатериалом.

Какие есть типы материалов:

брус или обрезная;
шпунтованная доска;
блок-хаусы и разные виды вагонки;
ОСБ плиты;
необрезная.

Для брусьев и обрезных принцип расчёта количества понятен и описан выше. При расчете количества и площади шпунтованных досок во внимание берутся только параметры их рабочей поверхности без учета выступающих гребней или пазов. На практике эта площадь соответствует площади укладки данных материалов, при том, что толщина остается стабильной.

Для блок-хаусов и вагонки предпочтительно использовать измерения в погонных метрах, как часто и делают большинство продавцов и изготовителей. Особенности разных деталей могут при измерении вызвать сложности.

ОСБ плиты также часто измеряют в погонных метрах, хотя объем кубатуры для них рассчитать достаточно легко.

Проблемным является расчет количества досок в 1 кубе, если рассчитываются необрезные и сложные детали, конструкции или изделия. Необрезные можно измерить в длину и толщину, а ширина их берется по усредненному показателю, то есть, она высчитывается, как среднее арифметическое ширины на обоих концах.

Существует разница при плотном и неплотном складировании, когда между пиломатериалами находится некоторое количество воздуха. Определенный подход к складированию вызван необходимостью поддерживать стабильную температуру и влажность внутри пиломатериалов, а при подсчетах кубатуры и количества в одном кубе будут высчитываться дополнительные коэффициенты, которые уточняют объем с поправкой на процент объема воздуха.

Иногда при расчете количества деталей сложной формы в одном кубометре могут прибегать к еще одному способу:

зная показатели плотности пиломатериалов из конкретной породы дерева при данных температуре и влажности, можно узнать объем 1 детали, взвесив ее и разделив на известную плотность.

Этот способ узнать, сколько в кубе досок, достаточно эффективен при условии, что известно значение плотности и другие показатели.

Таблица

Для большинства стандартных пиломатериалов предусмотрены стандартные табличные значения объемов, которые позволяют быстро и без длительных расчетов узнать количество досок в одном кубе. Для этого достаточно найти соответствующие значения в таблице, которая приведена во всех строительных учебниках.

Имея под рукой мобильный телефон или калькулятор, становиться возможным легко и быстро определить все количественные и объемные показатели. Однозначно пригодится для собственника нового жилья и знание описанных здесь уловок, на которые идут производители с целью повышения прибыли. Рациональный подход и математическая точность разрешат ряд проблем, помогая провести все ремонтно-строительные работы по плану и в срок.

Половая доска — сколько в кубе досок, как рассчитать нужное количество для строительства

Ход ремонта требует первоначального подсчета необходимого количества досок и средств для их приобретения.

Чтобы доски для пола хватило, нужно сделать правильные расчеты.

Давайте узнаем сколько в кубе досок

Свойственные размеры досок для пола

Во время выбора деревянных материалов для строительства для укладки на поперечной балки, исходят от толщины – наиболее животрепещущей характеристики ламелей.

Ламель шпунтованная

Какую толщину подобрать

Половые ламели выпускаются различной толщины (в мм):

Расчет доски для пола должен базироваться на том, с каким шагом установлены опоры.

Внимание! Экономия на конструкции поперечных балок приводит к переплате за намного толстые половицы.

На рисунке показано, какая рекомендованная величина толщины половиц указана в зависимости от расстояния между брусьями, чтобы они не деформировались и не сгибались.

Соотношение

Ширина и длина – основной параметр?

От толщины половицы зависит ее надёжность, а на что действует ширина и длина ламелей?

Ширина тоже бывает разнообразной – от 10 до 30-35 см. Чтобы напольное перекрытие выглядело красиво и представительно, применяются половицы лишь одной ширины.

И расчет длины имеет большое значение. При применении через чур длинных половиц – до шести метров, начнут появляться очаги скрипов из-за деформации, которая при подобных габаритах в первую очередь даст о себе знать.

Наиболее распространенные длины на строительном рынке:

Расчет расстояния между опорами поможет обойтись очень малым количеством отходов.

Сколько досок в кубе таблица

Предоставляем для вас обычную таблицу: сколько квадратов доски для пола в кубе.

Половичная толщина, мм	Укрываемая площадь пола одним кубометром доски, м2
20	50
25	40
30	33,3
35	28,5
40	25
45	22,2
50	20

Как видно из таблицы, 20-миллиметровые половицы покроют до 50 метров квадратных покрытия. При этом тут не берутся во внимание отходы из-за размещения опор.

Пример расчета

Можно высчитать, если исходить из этой таблицы, сколько в действительности покрытия потребуется, при применении ламели той либо другой толщины.

Представим, что брусья установлены с шажком в 60 см. Применение системы балок с подобным шагом комфортно, так как при обустраивании теплоизолированного пола это дает возможность класть между ними плиты и рулоны мин. ваты без надрезов и подгонки. Ведь минеральная вата имеет типовую ширину в 610 мм.

Можем считать, что поперечной балки с шажком в 60 см установлены из бруса сечением 100 ? 100 мм. Если исходить из указанного выше рисунка (таблицы), выходит, что понадобятся половицы в 35 мм.

Самая популярная длина досок – 6 м. Можем считать, что закуплена конкретно она.

Стало быть, одной доской в 6 метров можно покрывать от крайней поперечной балки до конечной расстояние в 565 см. При этом в конечную поперечную балку доска зайдет исключительно на половину ее ширины.

Сколько досок в 1 кубе

Выходит, что можно покрывать одним кубометром закупленной древесины (28,5*5,65)/6=26,8 метров квадратных покрытия. Отходов выходит 0,06 кубов.

Как видно, отходов вышло мало. В любом случае, расчет необходимого количества половой доски нужно будет делать индивидуально, если исходить из свойств установленных поперечных балок.

Сейчас ясно, как сосчитать, сколько досок для пола необходимо на пол:

поделить один кубометр на толщину половой доски;
получившуюся квадратуру разделять на ширину ламелей;
дабы получить кол-во ламелей, полученные погонные метры поделить на длину одной ламели.

Основное при расчетах – не путаться в величинах, чтобы нечаянно не прогадать.

Количество квадратов на шахматной доске

27. Сколько квадратов на шахматной доске или шахматной доске ?? (ответ не 64)

Можете ли вы расширить свою технику для вычисления количества прямоугольников на шахматной доске?

Еще одна головоломка, которую мне прислали по электронной почте через этот веб-сайт. Моим инстинктом было то, что ответ был просто большим, но я подумал об этом, и решение на самом деле довольно простое …

Прежде чем читать ответ, могу я вас заинтересовать подсказкой?

Во-первых, почему ответ не просто 64…
Все красные квадраты на картинке выше будут считаться действительными квадратами, поэтому мы спрашиваем, сколько квадратов любого размера от 1×1 до 8×8 есть на шахматной доске.

Ключ в том, чтобы подумать, сколько позиций может быть расположено в квадрате каждого размера … Квадрат 2×2, например, в силу своего размера может быть расположен в 7 положениях по горизонтали и 7 положениях по вертикали. т.е. в 49 различных позициях. Квадрат 7×7 может поместиться только в 2 положениях по вертикали и 2 по горизонтали.Рассмотрим, что ниже …

размер	горизонтальных позиций	вертикальных позиций	позиций
1х1	8	8	64
2х2	7	7	49
3×3	6	6	36
4×4	5	5	25
5×5	4	4	16
6×6	3	3	9
7×7	2	2	4
8×8	1	1	1
		всего	204

Всего на шахматной доске 204 клетки.Это сумма количества возможных позиций для всех квадратов размером от 1×1 до 8×8.

Формула для шахматной доски n x n?

Из приведенного выше анализа ясно, что решение в случае nxn представляет собой сумму квадратов от n ² до 1 ², то есть n ² + (n-1) ² + (n -2) ² … … 2 ² + 1 ²

Математически это записывается следующим образом:

Доказательство явного решения выходит за рамки этого сайта, но если вы хотите найти его, математик назовет его «суммой квадратов первых n натуральных чисел».’Окончательный ответ дает

n ³/3 + n ²/2 + n / 6

Можете ли вы расширить свою технику для вычисления количества прямоугольников на шахматной доске?

Ниже приведены некоторые примеры возможных прямоугольников …

Все приведенные выше примеры будут допустимыми прямоугольниками …

Есть несколько способов решить эту проблему. Но имеет смысл сначала расширить нашу технику от задачи о квадратах. Ключ к этому – думать о каждом прямоугольнике индивидуально и учитывать количество позиций, в которых он может быть расположен.Например, прямоугольник 3×7 может располагаться в 6 положениях по горизонтали и 2 по вертикали. Из этого мы можем построить матрицу всех возможных прямоугольников и суммы.

Размеры		1	2	3	4	5	6	7	8
	позиций	8	7	6	5	4	3	2	1
1	8	64	56	48	40	32	24	16	8
2	7	56	49	42	35	28	21	14	7
3	6	48	42	36	30	24	18	12	6
4	5	40	35	30	25	20	15	10	5
5	4	32	28	24	20	16	12	8	4
6	3	24	21	18	15	12	9	6	3
7	2	16	14	12	10	8	6	4	2
8	1	8	7	6	5	4	3	2	1
										1296

Всего существует 1296 возможных прямоугольников.

Элегантный подход к прямоугольникам, учтите вершины и диагонали.

Калпит Диксит прислал мне новаторское решение проблемы количества прямоугольников на шахматной доске. Это решение решает проблему с помощью другого подхода. Вместо того, чтобы смотреть на конкретные размеры прямоугольников и выяснять, где они могут быть расположены, мы начинаем с другого конца и сначала смотрим на места.

Вершины – это пересечения. Для нашей доски их 81 (9 х 9). Диагональ, начинающаяся в одной вершине и заканчивающаяся в другой, однозначно описывает прямоугольник.Чтобы быть диагональной, а не вертикальной или горизонтальной линией, мы можем начинать где угодно, но конечная точка не должна иметь одинаковые вертикальные или горизонтальные координаты. Таким образом, существует 64 (8 x 8) возможных конечных точек.

Таким образом, допустимые диагонали 81 x 64 = 5184.

Однако, хотя каждая диагональ описывает уникальный прямоугольник, каждый прямоугольник не описывает уникальную диагональ.

Мы тривиально видим, что каждый прямоугольник может быть представлен четырьмя диагоналями.

Итак, наше количество прямоугольников равно 81 x 64/4 = 1296

n x n или n x m?

Теперь можно вычислить n x n (например, 9×9,) или n x m (например, 10×15,) задач. Количество вершин определяется как (n + 1) ² и (n + 1). (M + 1) соответственно. Следовательно, окончательные решения таковы.

n x n: (n + 1) ² x n ²/4
n x m: (n + 1) x (m + 1) x (n x m) / 4

Что, очевидно, можно превратить во что-то более сложное.

Прямоугольники в математической номенклатуре

Я всегда стремлюсь объяснять проблемы без формальной математической терминологии, с аргументацией и здравым смыслом. Но здесь есть довольно изящное решение, если вы знаете о комбинациях, таких как перестановки и комбинации. По горизонтали выбираем 2 вершины из 9 имеющихся. Порядок не имеет значения, поэтому это комбинации, а не перестановки. И так же по вертикали. Таким образом, на проблему прямоугольника можно ответить следующим образом:

⁹ C ₂ • ⁹ C ₂ = 36 ² = 1296

© Найджел Колдвелл, 2004 г. – – вопросов на этом сайте могут быть воспроизведены без дополнительного разрешения, я не претендую на авторские права на них.Ответы принадлежат мне и не могут быть воспроизведены без моего явного предварительного согласия. Пожалуйста, задавайте вопросы, используя ссылку вверху страницы. Безопасная версия этой страницы.

Атрибуты и сети куба

Сводка

Учащиеся будут использовать свои знания об атрибутах кубиков, работать вместе в группах и находить как можно больше кубиков.

Материалы

Важная книга Инструкции:
	1. Сложите кусок плотной бумаги размером 12 x 18 дюймов пополам по горизонтали, затем откройте его и снова положите горизонтально.
	2. Затем снова сложите по вертикали 2 раза (сложите пополам и еще раз пополам)
	3.Разверните один раз. Разрежьте сгиб до средней линии сгиба и раскройте бумагу.
	4. Теперь сложите бумагу по горизонтали.
	5. Сожмите концы к центру, загните и загните.
	6. Буклет малый на 8 страниц. 1 страница – обложка 1 стр. – оборотная 6 внутренних страниц

Способы использования книги: Самое важное о: 3-м классе, новом друге, с которым я познакомился, дроби, геометрические фигуры и т. Д.(Отличная идея при использовании атрибутов.)

Дополнительные ресурсы

Книги

Важная книга Маргарет Уайз Браун ISBN: 0064432270

Фон для учителей

Куб состоит из шести квадратных граней, двенадцати ребер и восьми вершин. Когда квадратные грани куба разделены по краям и выложены плоско, они образуют двухмерную фигуру, называемую сеткой.Для куба существует одиннадцать различных сетей.

Сетка – двумерная фигура, которую можно сложить в трехмерную фигуру, является сеткой этой фигуры.
Лицо – плоская фигура, служащая одной стороной твердой фигуры. Грани куба – квадраты.
Вершина (вершины) – точка, в которой два отрезка, прямые или лучи встречаются, образуя угол.
Ребро – отрезок прямой, на котором встречаются две грани твердого тела.

Сегодня ученики будут использовать свои знания об атрибутах кубиков, работать вместе в группах и находить как можно больше способов сделать куб. Двумерный узор для трехмерной формы называется сеткой.

Ученики будут работать вместе в небольших группах, и каждая группа будет разного цвета. Они будут использовать ленту, чтобы соединить фигуры, которые складываются в куб.

Предполагаемые результаты обучения

1.Продемонстрировать положительное отношение к математике.
2. Научитесь решать математические задачи.
3. Рассуждайте математически.

Инструкционные процедуры

Приглашение к учебе
Выведите учащихся на площадку. Спросите: «Кто может сказать, что такое атрибут? Атрибут описывает что-то о предмете или человеке. Попросите ученика встать перед классом и назвать атрибут ребенка (цвет его волос, глаз, обуви, и т.п.). Сегодня мы узнаем об атрибутах куба.

Прочтите книгу « Важная книга » Маргарет Уайз Браун.

Скажите студентам, что, как детективы, они будут описывать атрибуты куба.

Инструкционные процедуры

В классе выберите двух- или трехмерный объект в классе (например, глобус или флаг). Попросите учащихся придумывать атрибуты, а учитель перечисляет атрибуты на доске.
Поднимите куб и обсудите с учениками различные атрибуты куба, убедившись, что они называют «боковые» грани. Попросите студентов записать атрибуты в своих математических журналах.
Попросите учащихся осмотреть комнату и назвать предметы, имеющие форму куба. Проверьте заранее и убедитесь, что у вас есть хотя бы один или два кубических объекта в комнате! Если это не было затронуто, спросите учащихся, какие двухмерные формы составляют куб.
Затем просмотрите атрибуты куба.Запишите их на доске. Попросите учащихся записать их в своих дневниках.
Затем предложите учащимся объяснить, почему, по их мнению, форма куба важна. Попросите их придумать в реальной жизни предмет, имеющий форму куба, и перечислить его атрибуты. Попросите учащихся заполнить рабочий лист «Важная вещь». Заполнив лист, студенты могут составить буклет со своими атрибутами.
Затем учащиеся работают в группах по четыре человека, используя двухдюймовые квадраты, чтобы создать как можно больше различных сеток для куба.Дайте каждой группе два набора по 6 штук, чтобы у каждого в группе была возможность опробовать свои идеи. Как только они подумают, что у них есть сеть, попросите их доказать, что она работает, скопировав сеть на 2-дюймовую сетку, вырезав ее и сложив в куб. Возможно, вы захотите показать всему классу несколько первых рабочих сетей, которые являются Вы можете принять участие в соревновании, чтобы учащиеся сосредоточились. Побеждает группа с самыми разными сетками для куба.

Закрытие

В математических журналах пусть ученики подходят к классу и записывают атрибуты сетей.

Каждая сетка состоит из шести квадратов, которые при правильном сложении образуют шесть граней куба.
Для каждой сети шесть граней соединены пятью ребрами. Попросите учащихся поделиться и записать то, что они узнали о кубе.
Кубики имеют двенадцать граней
восемь вершин
шесть граней

Оценка

Учащиеся могут рисовать на миллиметровой бумаге различные способы, которые они нашли для создания сети.
Студент Важная книга о кубе.
Записи журнала.
Учащиеся создают буклет, демонстрирующий знание атрибутов куба.

Расширения

Расширение учебной программы / адаптации / интеграция

Отлично подходит для интеграции языковых навыков и письма в математику

Семейные связи

Учащиеся отправляются на поиски «кубиков» у себя дома.

План оценки

Библиография

Основа исследования

Битти В., Коллинз Б. и Макиннес Б. (1997). Глубокое и поверхностное обучение: простая или упрощенная дихотомия? Бухгалтерское образование , 6 (1), 1-12.

Стихи глубокого обучения на поверхности или зубчатое заучивание имеют важное значение для учащихся, чтобы получить понимание для обучения.Процессы обучения студентов для глубокого обучения включают использование различных стилей обучения для улучшения личности студента.

Хартсхорн Р. и Борен С. (июнь 1990 г.). Практическое изучение математики: Использование манипуляторов. Вашингтон, округ Колумбия: Информационный центр ERIC по сельскому образованию и малым школам, ERIC Digest. (Номер услуги репродукции документов ERIC ED321967)

Активное участие в различных стилях обучения улучшит обучение студентов. Математика настолько абстрактна, что ученикам становится трудно ее понять.Следовательно, использование манипуляторов имеет важное значение для обучения.

Создано: 27.06.2006
Обновлено: 05.02.2018

108153

сколько квадратов в кубе

Квадрат 2 * 2 будет иметь 4 + 1 квадрата и 4 прямоугольника, то есть как долго будут длиться следы на Луне? Обе являются прямоугольными призмами, у которых должно быть 6 граней. Например, 53 = 5 × 5 × 5, а 82 = 8 × 8.Инструкции по использованию онлайн-калькулятора квадратов и кубов довольно просты. Одно не может быть преобразовано в другое. Куб двойственен октаэдру, имеет кубическую или октаэдрическую симметрию. Совершенные квадраты: 1, 4, 16, 25 Вот несколько простых приемов вычисления куба числа. а. 1 равно 12 и 13. Куб с длиной ребра 4 сантиметра имеет объем 64 кубических сантиметра, который мы можем записать как 64 см3. Обязательно плотно прижмите каждую складку, чтобы получилась четкая складка.2 и получилось 361. Куб имеет длину стороны 4 см. Экспоненты также используются для обозначения единиц площади (квадратных единиц) и единиц объема (кубических единиц). У каждого маленького кубика длина стороны равна 1 единице. Следовательно, в квадрате 4×4 есть $ 2 \ times 2 = 4 $ 3×3 квадрата. Вы можете образовать четырехугольники большего размера, соединив 4 вершины любого из квадратов. Учебную программу по математике Open Up Resources можно бесплатно загрузить с веб-сайта Open Up Resources, а также можно получить в Illustrative Mathematics. Магия химии потоков, черные дыры и, возможно, причина смерти динозавров (см. Ниже).(Ошибка в названии апплета.) Есть и другие правильные многогранники (тетраэдр, октаэдр и т. Д.). Решение загадки «Сколько квадратов», которая часто всплывает на шкале времени Facebook. Ниже приводится список идеальных квадратов. Квадраты. Введите точное число. (Б) Сколько квадратов находится на всех сторонах куба? 2. Для вычисления всех математических решений квадрата и куба калькулятору квадратов и кубов требуется только одно из значений квадрата. Идеальные кубики. Вернемся к факторингу.Серый квадрат даст вам 32 кубика. Поскольку 4 × 4 × 4 равно 64, мы можем написать 43 = 64 и сказать: «4 в кубе – это 64». 4 x 16 = 64 – это произведение двух квадратов, поэтому это тоже квадрат. Хорошее знание этого имеет решающее значение почти во всех конкурсных экзаменах, таких как SSC CHSL, RRB NTPC, IBPS RRB PO / Clerk,… Copyright © 2005, 2020 – OnlineMathLearning.com. Если переменная с показателем степени имеет четный показатель, то это полный квадрат. Некоторые примеры показаны на картинке выше. Построенный куб состоит из 64 кубиков привязки.Однако это будет неточно, поскольку куб – это не все кубики. Будьте конкретны и при необходимости пометьте диаграмму. 4. Повышенная 2 из 52 называется экспонентой. Закон квадратного куба просто указывает, что объем растет экспоненциально быстрее, чем площадь поверхности с увеличением размера, поскольку площадь является квадратной функцией, а объем – кубической функцией. Квадрат со стороной 5 дюймов имеет площадь 25 квадратных дюймов, которую мы можем записать как 25 дюймов2. Встроенный контент, если таковой имеется, является собственностью соответствующих владельцев.Engineering ToolBox – ресурсы, инструменты и основная информация для проектирования и разработки технических приложений! Какое количество рассчитывается путем умножения трех измерений длины, ширины и высоты? 3. Итак, 9 умножить на 6 равно 54. Куб имеет 48 симметрий, 24 из которых могут быть физически реализованы на твердом кубе; остальные 24 фактически выворачивают куб наизнанку. Каков объем построенного куба? Напишите предложение, объясняющее ваши рассуждения. В частности, когда Куб расшифровывается отдельно от ориентации центральных квадратов, всегда будет четное количество центральных квадратов, требующих четверти оборота.Источник (и): У меня классический кубик Рубика. 4. Мы можем записать это как 43. Четность. Куб – единственный правильный шестигранник и одно из пяти Платоновых тел, у него 6 граней, 12 ребер и 8 вершин. их 9… Мы приветствуем ваши отзывы, комментарии и вопросы об этом сайте или странице. 1. Вставьте угол в деталь, которую вы вставляете, чтобы прикрепить его. Имеется 840 квадратов и 3864 прямоугольника для кубика рубика 7 × 7. 3. 1) Всего у вас есть 9 квадратов, расположенных так, чтобы образовывать… Пробовав вопросы, нажмите кнопки, чтобы просмотреть ответы и пояснения в тексте или видео.3 – простое число и не идеальный куб. Это дает еще 10 квадратов, так что всего на картинке 30 + 10 = 40 квадратов. На иллюстрации внизу слева показаны две… Первый изготовленный кубик Рубика имел шесть сторон, каждая из которых разного цвета (традиционно синий, зеленый, оранжевый, красный, белый и желтый). Методы сложения чисел от 1 до 100; Переосмысление арифметики: наглядное руководство; Краткое понимание: интуитивное значение… Каков ответ на увлекательную школьную математическую книгу e-28? Мы можем построить модель куба и посчитать его 8 вершин, 12 ребер и 6 квадратов.Построенный куб имеет длину стороны 3. 6. a. Совершенные квадраты и идеальные кубики. Мы можем записать его как 43. Эти точки лежат в строках и столбцах, как на рисунке. Давайте исследуем совершенные квадраты и идеальные кубы. Число 27 – идеальный куб. Закон квадрата-куба (или закон куба-квадрата) – это математический принцип, применяемый в различных областях науки, который описывает взаимосвязь между объемом и площадью поверхности по мере увеличения или уменьшения размера формы. Подобно квадратным корням, кубические корни – это операции, обратные кубам.3 = 27 кубиков, и только один из них (центральный) не выставлен. Найдите четыре числа, которые являются полными квадратами, и два числа, которые не являются полными квадратами. Мы используем слово в кубе для обозначения «в третьей степени». У квадрата длина стороны 4 см. Если это… Использование калькулятора. а. Как и идеальные квадраты, число является идеальным кубом, когда из этого количества маленьких кубиков можно собрать больший куб. Из предыдущих вопросов, куб объемом 27 кубических единиц имеет размер 3 × 3 × 3, а куб объемом 64 кубических единицы имеет размер 4 × 4 × 4.Площадь любой грани построенного куба составляет 4 × 4 = 16 квадратных единиц. • Запишите на доске, как учащиеся смотрят на вещи, в стиле разговоров с числами: напишите «Учащийся» Почему библиотеки не пахнут книжными магазинами? Используйте свои знания о таблицах умножения или умножении 10: если число в списке не является результатом умножения числа на себя, это не идеальный квадрат. Например, начните с 4 квадратов в линию и одного на конце, образуя l-образную форму. Чтобы получить квадратный корень, мы просто делим показатель степени на 2.Сколько кубов разного размера (например. В контексте | geometry | lang = en) разница между квадратом и кубом заключается в том, что квадрат (геометрия) представляет собой многоугольник с четырьмя сторонами равной длины и четырьмя углами по 90 градусов; правильный четырехугольник, у которого все углы равны 90 градусов, в то время как куб (геометрия) представляет собой правильный многогранник с шестью одинаковыми квадратными гранями. 2. a. 361 и 324 – идеальные квадраты. Начнем с самой низкой. Давайте возьмем любую грань 1 * 1 квадратов = 25 как одну грань. куб состоит из 25 крошечных кусочков квадратов 2 * 2 квадрата = 16 Если у вас возникли трудности с визуализацией этого.Мы знаем, что четырехмерный гиперкуб имеет 16 вершин, но сколько ребер, квадратов и кубов он содержит? Повторите то же самое с четырьмя квадратами в линию и пятым квадратом, образуя букву «т»… Сколько квадратов на кубике рубика? Синий всегда будет противоположным Зеленому. Различные типы кирпичей служат разным целям, включая изоляцию, термостойкость для… Сколько сетей вы можете найти…… Это 5 × 5 × 5 (5 × 5 для одной стороны – что в терминологии куба – это слой), а затем 5 слоев. Посчитайте: 9 * 6 – 12 – 8 * 2 = 26.Когда мы умножаем три одинаковых числа вместе, как 4 × 4 × 4, мы говорим, что кубизируем это число. Призма А имеет размер 3 дюйма на 2 дюйма на 1 дюйм. Также важно познакомить пользователя… квадраты 1 + квадраты 2 будут количеством квадратов, а квадраты и прямоугольники вместе будут кубом 2, что составит общее число девять. Какая у него длина стороны? Как рассчитать квадраты? Когда органная музыка стала ассоциироваться с бейсболом? Чтобы читать 25 дюйм2, мы говорим «25 квадратных дюймов», как и раньше. Подсчитайте квадраты, кубы или гиперкубы В квадратной сетке точек вы можете рисовать, соединив любые две точки линией.Когда студенты нашли и записали все 11 (возможно, таким образом, чтобы показать «самые длинные линейные семейства»), остается еще несколько возможных исследований. Выберите все утверждения о двух призмах, которые верны. Решите, является ли каждое число в списке идеальным кубом. Используйте столько кубиков, сколько вам нужно, чтобы построить самый большой из возможных кубов. Какой многогранник можно собрать из этой сетки? Площадь призмы B = 4 (6) + 2 (1) = 26 кв. Дюймов. Но (их … Рассмотрим центральный квадрат на каждой грани. Ответ зависит от того, разрешено ли перекрытие бумаги.Кстати, есть формула для подсчета количества квадратов в сетке n x n. Найдите четыре других числа, которые являются идеальными кубиками, и два числа, которые не являются идеальными кубиками. В контексте | математики | lang = en terms… Вопрос: – «Сколько квадратных дюймов в кубическом футе?» В кубическом футе нет квадратных дюймов. Теперь посчитайте количество квадратов, образованных двумя средними квадратами. Закон квадрата-куба (или закон куба-квадрата) – это математический принцип, применяемый в различных областях науки, который описывает взаимосвязь между объемом и площадью поверхности по мере увеличения или уменьшения размера формы.Когда мы умножаем два одинаковых числа вместе, например 5 × 5, мы говорим, что возводим число в квадрат. Как видно из объяснения D выше, призма B имеет большую площадь поверхности, чем призма A. Студенты; младшие школьники 5-11 лет; средний возраст 11-18 учеников средней школы; Публикация 16 лет 16+ публикация 16; Учителя; ранний возраст 0-5 лет Ранние годы; … Всего вы умножаете 9 на 6, и получается 54 наклейки. Сделайте то же самое для куба 4 x 4 x 4, куба 5 x 5 x 5 и куба n x n x n. Число – это идеальный куб, когда из этого количества маленьких кубиков можно собрать больший куб.Площадь квадрата со стороной 7 км составляет 72 км2. Привет, Арул. 2. Идеальные кубики: 1, 8, 64, 125 Построенный куб состоит из 27 кубиков оснастки. Пропустить навигацию. Однако, если вы спрашиваете, как в математической головоломке, например, говоря, что блок 2×2 является квадратом, а затем сам куб является квадратом, а сами маленькие квадраты являются квадратами, и вы спрашиваете, сколько их, их 108 если вы считаете 2-х мерные квадраты. Вы можете использовать это так: (мы говорим «кубический корень из 27 равен 3»). Вы также можете кубить отрицательные числа.квадраты 1 + квадраты 2 будут количеством квадратов, а квадраты и прямоугольники вместе будут кубом 2, что составит общее число девять. т.е. 2. Задача: Дан куб 2 x 2 x 2, состоящий из 8 блоков 1 x 1 x 1. Кубик Рубика состоит из 26 маленьких кубиков (внутри пазла кубиков нет). Например, вы можете сложить вверх по всем линиям. 1. Поскольку упрощение является важной частью количественных способностей, мы узнаем, как знать квадраты, кубы, квадратный корень и кубический корень.Это потому, что квадрат со стороной s имеет площадь s × s, или s2. Квадраты, кубы, квадратные корни и куб… Чтобы найти ответ, сначала мы должны знать, что куб – трехмерный твердый объект, ограниченный шестью квадратными гранями, гранями или сторонами, и он равен со всех сторон. В базе два нуля, поэтому будет добавлено до 2 цифр. Простое число – это число с ровно двумя множителями. 343 – идеальный куб. Всего 45 кубиков. Какая у него длина стороны? 1. 4. c. Оранжевый всегда будет противоположен Красному.Какова длина ребра построенного вами куба? Итак, приступим. Совершенные квадраты и идеальные кубики. 32 – не идеальный куб. Я продолжал это делать, пока не получил число меньше 315, записывая все, что было между ними. Итак, теперь мы добавляем дополнительные 5 × 5 = 25 кубиков в верхний ряд. Другой способ… Каков его объем? Итак, здесь, на изображении головоломки, мы видим, что нам нужно сложить 2 куба в верхнем ряду, 6 кубиков… 3. Мы используем слово в квадрате для обозначения «во второй степени». Продолжить чтение. Мы также можем сказать, что 25 – это идеальный квадрат.W (a) Сколько квадратов на желтой стороне куба? Это равно количеству используемых кубиков привязки. Кубики и кубические корни. Масштабирование отношения площади поверхности к объему в масштабе квадратного куба объясняет, почему на сковороде сушится быстрее, чем на… 3. a. Квадрат со стороной 5 дюймов имеет площадь 25 кв. Это также идеальный куб, потому что он равен 253. Сначала ответьте на вопросы 1 и 2. Если… Покажи свою аргументацию. Главное меню Поиск. Все складки должны быть в одном направлении. 2. Другой способ выразить это так: идеальный куб – это результат возведения любого целого числа в третью степень.Сколько кубиков оснастки вы использовали? Задача: дан куб 2 x 2 x 2, состоящий из 8 блоков 1 x 1 x 1. Квадрат имеет длину стороны 7 км. «Куб» – это трехмерный объем. E: Площадь поверхности призмы B больше, чем у призмы A. Perfect Cubes. Интервью для инженера-разработчика программного обеспечения из Макати. Сколько квадратов в кубике рубика? Какова его площадь? Используйте показатель степени, чтобы выразить его объем. Кстати, есть формула для подсчета количества квадратов в сетке n x n. Рекламные ссылки .Что 84 делится на 26 делится на равные части. Неидеальные кубики: 9, 16 Они говорят вам, на сколько факторов нужно умножить. Если нарисован куб 3 x 3 x 3, то у данного блока могут быть нарисованы 0, 1, 2 или 3 грани. Итак, если мы говорим о кубах (отдельные части, составляющие b. Площадь двух наклонных граней = 2 × 1 м × 1,2 м = 2,4 м2 Ребра гиперкуба делятся на четыре группы по 8 параллельных ребер. Когда мы умножаем два одинаковых числа вместе, например 5 × 5, мы говорим, что возводим число в квадрат.Число представляет собой идеальный квадрат, когда из этого количества маленьких квадратов можно составить большой квадрат: Откройте апплет. Сколько существует положительных двузначных чисел, у которых квадрат и куб оканчиваются на одну и ту же цифру? Используйте это длинное … Используйте столько из них, сколько вам нужно, чтобы построить самый большой отдельный куб, который вы можете. На одной стороне кубика Рубика 9 квадратов (или наклеек). Эту сетку можно собрать в треугольную призму. Осталось 5 кубиков оснастки. Используя этот метод, мы можем вычислить следующий квадрат, который является кубом, повторяя этот процесс.D: Две призмы имеют одинаковую площадь поверхности. Но мы можем пойти еще дальше. Обязательно укажите правильные единицы измерения в каждом ответе на эти вопросы. Требуются длины сторон прямоугольников (s1, s2, s3 и s4) и высота треугольников h. Покажи свои рассуждения. Вероятно, это самый простой способ найти решение. Представьте, что вы выращиваете куб (сделанный из гальки!) 4. Квадрат 2 * 2 будет иметь 4 + 1 квадрата и 4 прямоугольника, т.е. все размеры указаны в метрах. 1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81 10 2 = 100 11 2 = 121 12 2 = 144.Поднятое 3 в 43 также является показателем. Для числа x кубический корень x – это такое число a, что a 3 = x. Если x положительный, a будет положительным, если x отрицательным, a будет отрицательным. 1. Правильно сориентируйте куб. Точно так же квадраты можно рассматривать как шесть групп из 4 параллельных квадратов, по одному квадрату через каждую вершину. Определенные пары центральных квадратов (и по умолчанию определенные пары цветных граней) всегда будут противоположны друг другу. Примечание. Числа, которые при вычислении квадратного корня дают целые числа, называются идеальным кубом.Мне сложно это понять. Идеальные квадраты. Это список квадратов и кубиков от 1 до 50. 2. Какова площадь каждой грани построенного куба? Впервые он был описан в 1638 году Галилео Галилей в его «Двух новых науках» как «… соотношение двух объемов больше, чем соотношение их поверхностей». 0 0. Мы также используем это обозначение для квадратных и кубических единиц. Вернемся к факторингу. На красном кубе 6 квадратов и 6 на синем, и мы также находим 12 квадратов, очерченных краями движущегося куба, всего 24.Найдите другое число, которое одновременно является идеальным квадратом и идеальным кубом. Идеальные квадраты. Наконец, мы добавили 25 недостающих кубов плюс 25 недостающих кубов наверху. Показать транскрибированный текст изображения. У них также по 9 квадратов с каждой стороны, поэтому 6 * 9 = 54. Всего вы умножаете 9 на 6, и получается 54 наклейки. Чтобы понять кубические корни, сначала мы должны понять кубики … Как кубировать число. B: Верно. Построенный куб имеет длину ребра 4. Первые пять положительных идеальных кубов – это 1, 8, 27,… Неидеальные квадраты: 5, 24 Поскольку 4 × 4 × 4 равно 64, мы можем написать 43 = 64 и сказать: «4 в кубе – это 64».Запишите те возможности, которые создают кубические сети. Призма B имеет размер 1 дюйм на 1 дюйм на 6 дюймов. Так что да, 9 умножить на 6 равно 54. Попробуйте эти примеры или введите свой собственный. Покажи свои рассуждения. Попробуйте бесплатный калькулятор Mathway и 5. Куб также представляет собой квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр. Это правильная квадратная призма в трех ориентациях и треугольный трапециевидный элемент в четырех ориентациях. То, что началось как подвижный прототип, вскоре поможет его студентам-архитекторам стала самой продаваемой игрушкой, ведущей к мировым чемпионатам по разгадыванию головоломок, побочным продуктам и спидкубингу.Мы можем записать выражение как 52.

Скрытых прямоугольников

Получено аккуратное решение первой части задачи от Саны, Дженни, Криса и Розион из Мадрасского колледжа, Сент-Эндрюс. Мне нравится использовать линии, а не думать о прямоугольники точно так же, как и квадраты (что я и сделал). Эту идею довольно легко обобщить на шахматы размером n x n. доска.

Остальные верные решения были получены от Андрея из школы 205. Бухарест, средняя школа общины Мэри Берчвуд и Чен из Китайская средняя школа, Сингапур.

Молодец.

На шахматной доске 1296 различных прямоугольников.

204 из этих прямоугольников – квадраты.

Первый взгляд на квадраты:

Рассмотрите возможность размещения квадрата размером 1 x 1 вдоль левого края. шахматной доски. Этот квадрат может находиться в любой из 8 позиций (как на шахматной доске 8 на 8 квадратов). Аналогично квадрат может быть размещен в любом из восьми положений по верхнему краю. Так общее количество

1 x 1 квадрат = 8 x 8 = 64.

Квадрат 2 x 2 может занимать 7 позиций по левому краю. и 7 позиций по верхнему краю 7, что дает 7 x 7 = 49 квадратов размер 2 x 2.

Продолжая таким образом, мы получаем квадраты размером 3 x 3, 4 x 4 и скоро.

Размер квадрата	Кол-во квадратов
1 х 1	8 х 8 = 64
2 х 2	7 x 7 = 49
3 x 3	6 х 6 = 36
4 х 4	5 х 5 = 25
5 x5	4 х 4 = 16
6 х 6	3 х 3 = 9
7 x 7	2 х 2 = 4
8 х 8	1 х 1 = 1

Итак, есть 204 квадрата.

Затем, глядя на прямоугольники:

На шахматах 9 вертикальных и 9 горизонтальных линий. доска.

Чтобы сформировать прямоугольник, вы должны выбрать 2 из 9 вертикальных линий. и 2 из 9 горизонтальных линий.

Для двух горизонтальных линий: первую строку можно выбрать в 9 способов второй – восемь способов. Это означало бы, что вы могли сказать разница между строками 1 и 3, скажем, и 3 и 1, что не случай, поэтому вам нужно разделить 9 x8 8 на 2, получив 36.

Аналогичным образом вы можете выбрать две вертикальные линии 36 способами.

Итак, количество прямоугольников равно 362

362 = 1296

Следующий подход использует несколько других решений отправлено.

Прямоугольник (или квадрат) будет иметь высоту от 1 до 8 единиц. и шириной от 1 до 8 единиц. Это можно представить в виде таблица с каждой возможной шириной, представленной столбцом, и каждый восемь подряд.

Записи в таблице ниже указывают количество каждого прямоугольник на шахматной доске (используя аргументы, аналогичные первым часть проблемы выше).

В последнем столбце таблицы указано общее количество прямоугольники в каждой строке.

Высота / ширина	1	2	3	4	5	6	7	8	Всего
1	8 х 8	7 х 8	6 х 8	5 х 8	4 х 8	3 х 8	2 х 8	1 х 8	8 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8} = 8 x 36
2	8 х 7	7 х 7	6 х 7	5 х 7	4 х 7	5 х 7	2 х 7	1 х 7	7 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8} = 7 x 36
3	8 х 6	7 х 6	6 х 6	5 х 6	4 х 6	3 х 6	2 х 6	1 х 6	6 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8} = 6 x 36
4	8 х 5	7 х 5	6 х 5	5 х 5	4 х 5	3 х 5	2 х 5	1 х 5	5 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
5	8 х 4	7 х 4	6 х 4	4 х 4	5 х 4	3 х 4	2 х 4	1 х 4	4 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
6	8 х 3	7 х 3	6 х 3	4 х 3	5 х 3	3 х 3	2 х 3	1 х 3	3 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
7	8 х 2	7 х 2	6 х 2	4 х 2	5 х 2	3 х 2	2 х 2	1 х 2	2 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
8	8 х 1	7 х 1	6 х 1	4 х 1	5 х 1	3 х 1	2 х 1	1 х 1	1 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
									(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8} x 36 = 362

Следовательно, общее количество прямоугольников в сетке 8 x 8 равно (1 + 2 + 3 +… + 8) 2

Общее количество прямоугольников в сетке n x n составляет (1 + 2 + 3 + … + п) 2 = (п2 (п + 1) 2) / 4. Это использует формула суммы первых n натуральных чисел, арифметическая прогрессия. Подробнее об этом см. В доказательстве. сортировщик (ссылка).

Количество квадратов: (12 + 22 + 32 + … n2) = (n (n + 1) (2n + 1)) / 6 (для доказательства см. телескопирование серия)

SA: Имеют ли кубы и квадраты те же свойства, что и сферы и круги?

Студенты-математики часто бывают заинтригованы, когда понимают, что производная формулы объема сферы по радиусу сферы является формулой поверхности сферы:.Они также очарованы тем фактом, что производная от формулы площади круга является формулой для его длины:. Эти результаты, кажется, неприменимы к кубам и квадратам, потому что площадь поверхности куба и периметр квадрата. Почему сферы и круги ведут себя так, а кубы и квадраты – по-другому?

Рассмотрим производную площади круга. Согласно определению производной:

Геометрически этот результат легко увидеть, потому что область между двумя концентрическими окружностями, одна с радиусом r и другая с радиусом r + h , по существу представляет собой полосу шириной h и длиной 2π r , как показано на рисунке 1.

Аналогичное вычисление справедливо для производной объема сферы. Согласно определению производной:

Геометрически этот результат легко понять, потому что область между двумя концентрическими сферами, одна с радиусом r, а другая с радиусом r + h , по существу представляет собой полый шар толщиной h и площадью поверхности 4π r ².

Подобные результаты не верны для стандартной формулы для объема куба и площади квадрата, как показано в первом абзаце.Давайте рассмотрим различные формулы: Пусть s будет расстоянием от центра квадрата перпендикулярно противоположной стороне, как показано на рисунке 2. Тогда, поскольку s составляет половину длины края квадрата, мы имеем формула A = (2 с ) ² = 4 с ² и P = 8 с для площади квадрата и периметра квадрата соответственно.

Рассмотрим производные этой новой формулы площади квадрата.Так как A = 4 с ², что является нашей формулой для периметра квадрата. Аналогично, пусть s будет расстоянием от центра куба перпендикулярно противоположной стороне. Тогда, поскольку s составляет половину длины ребра куба, мы имеем формулу V = (2 s ) ³ = 8 s ³ для объема куба, и (2 с ) ² = 4 с ² для площади каждой грани.Поскольку V = 8 с ³, то, что в 6 раз превышает площадь грани куба, и, таким образом, это выражение равно площади поверхности куба. Записав формулы в терминах s , половина длины ребра, мы теперь имеем формулы, которые имеют свойства, согласующиеся со свойствами сфер и кругов.

Мы можем распространить этот результат на равносторонние треугольники. Пусть e будет длиной ребра треугольника, как показано на рисунке 3.

Площадь треугольника равна, а его периметр равен 3 e . Производная площади равна, что отдаленно не похоже на периметр треугольника. Давайте теперь изменим переменную и пусть s представляет собой перпендикулярное расстояние от центра треугольника до одной из сторон, как показано на рисунке 4.

Используя соотношение Пифагора, или. В единицах s площадь треугольника равна, а периметр равен. Поскольку производная площади равностороннего треугольника равна периметру треугольника.Рисунок 5 показывает, что разница между треугольными областями с использованием s и s + h , по сути, представляет собой трехстороннюю полосу шириной h и длиной, равной периметру треугольника, что геометрически подтверждает наш результат.

Случай равностороннего треугольника предлагает способ обобщения этого результата на другие правильные многоугольники. Отрезок s от центра многоугольника перпендикулярно стороне называется апофемой многоугольника.Тогда длина стороны многоугольника равна, где n – количество сторон, и, следовательно, периметр многоугольника равен. Площадь многоугольника – это длина апофемы, умноженная на половину длины периметра. В символах:

Теперь мы можем проверить это, периметр правильного многоугольника.

Предложите своим ученикам применить этот метод к правильному шестиугольнику. Они должны найти формулы для площади и периметра шестиугольника с точки зрения его апофемы.Затем они должны показать, что одно является производным от другого.

Мы также можем распространить наши результаты на трехмерные фигуры. Для правильных многогранников апофема – это радиус вписанной сферы. Рассмотрим тетраэдр.

Стандартные формулы для объема и площади поверхности тетраэдра обычно основаны на длине ребра, a , тетраэдра. Однако нетрудно переписать их в терминах длины r апофемы – радиуса вписанной сферы.

r = радиус вписанной сферы = апофема многогранника
R = радиус описанной сферы
a = длина края тетраэдра
S = площадь поверхности тетраэдра
V = объем тетраэдра

В пересчете на r вписанный радиус:

Таким образом, мы легко можем видеть, что в терминах апофемы производной формулы для объема тетраэдра является формула для его площади поверхности.

Аналогично, используя стандартные формулы для объема и площади поверхности октаэдра на основе длины ребра, a , октаэдра. Мы можем переписать их в терминах длины апофемы r .

Опять же, ясно, что производная формулы объема относительно r является формулой для площади поверхности.

Вот формулы для объема и площади поверхности двух других правильных многогранников через длину вписанного радиуса, r .

Додекаэдр:

Икосаэдр:

Вы можете поручить учащимся сложную задачу проверки того, что производная приведенной выше формулы для объема додекаэдра на самом деле является данной формулой для его площади поверхности.

Какова ценность этого результата? Это просто академическое упражнение? Фактически, эти формулы предоставляют простой способ найти формулу для площади поверхности обычных твердых тел, если вы знаете формулу для их объема, или наоборот.Просто напишите формулу в терминах апофемы твердого тела и дифференцируйте или антидифференцируйте соответственно, чтобы найти другую формулу.

Список литературы

http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html#octahedron

http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html

Джон Ф. Махони представил AP Statistics в средней школе Banneker в 2002–2003 годах и обучил 59 студентов в этом году в рамках курса. Каждый из студентов сдавал экзамен AP, и Махони считает, что у них, возможно, был самый высокий процент пожилых людей, сдающих статистику AP в стране.В этом году он также преподает исчисление AP уровня AB и BC. Он является консультантом AP и давним участником чтения AP Calculus. В настоящее время он является одним из руководителей экзаменов. Он также возглавляет редакционную коллегию журнала NCTM ON-Math: www.nctm.org/onmath. В средней школе Баннекера он является одним из наставников команды робототехники и помогает студентам проектировать приводные механизмы на основе зубчатых колес – так же, как сам Баннекер делал более 200 лет назад. Им помогают многие инженеры, в том числе из Университета Ховарда, расположенного через проспект Джорджии от средней школы.Он является одним из тренеров отмеченной наградами школьной команды It’s Academic. Когда он решил преподавать в средней школе Баннекера три года назад, после долгой карьеры в частных школах, он изучил математику Баннекера, и эта статья является результатом этой работы.

Картонный куб

Создание идеального картонного куба 3 “x 3”

Будьте осторожны, чтобы не порезать столы и не наклеить клей. их.

Соберите материалы, которые понадобятся вам для этого упражнения.
- упаковка лезвий Exacto и нож Exacto
- металлическая прямая кромка
- твердая режущая поверхность (может быть режущая поверхность Exacto, деревянная доска, так далее)
- 30-60-90 или 45-45-90 треугольник
- клей белый
- лист картона
Ознакомьтесь с используемым материалом, то есть с картоном.
- Посмотрите на картон и поймите
- Обратите внимание на его конструкцию. Обратите внимание, что у него есть зернистость. Картон:
  - состоит из трех слоев: ребристая внутренняя структура, зажатая между двумя гладкими гранями;
  - – сильнейший, параллельный гребням; а также
  - – самый слабый перпендикуляр к гребням.
- Возьмите кусок картона. Используя металлическую линейку в качестве направляющей, разрезать картон новым лезвием.
  - Не применяйте сильное давление; Не пытайтесь прорезать картон все сразу.
  - Попробуйте прорезать только один слой, не разрезая другие слои.
  - Попробуйте прорезать всего два слоя, не разрезая третий слой.
  - Обратите внимание, как легко острое лезвие разрезает картон всего за несколько удары.
  - Подумайте, какая сторона разреза является хорошей, а какая сторона будет в утиль.Положите металлическую направляющую на хорошую сторону, чтобы что если ваш нож поскользнется, он порежет ту сторону, которая будет слом.
Сделайте куб
Когда вы закончите с шагами в этом разделе, у вас должен быть Картон 6 штук. Квадраты, которые будут 4 сторонами куб должен иметь вырезы 1/8 дюйма на 3 края. Верх и низ должны быть 3-дюймовыми квадратами без вырезов.
1. Постройте четыре стороны
  1. Замените лезвие Exacto.
  2. Сделайте чистый прямой пропил около одного из краев. Сделайте еще один чистый прямой надрез перпендикулярно первому надрезу и близко к соседнему краю. Убедитесь, что угол, образованный этими двумя разрезами, перпендикулярен.
    - Используйте треугольник, чтобы убедиться, что у вас прямой угол.
    - Примечание: этот шаг необходим, потому что края листа картона часто давятся. Мы хотим чисто, прямо края.
    - Примечание: Используйте только металлическую прямую кромку при обрезке картон ножом Exacto. Не используйте треугольник как прямая кромка: острое лезвие испортит кромку треугольник (если вы не используете металлический треугольник).
  3. Из этого установленного угла вырежьте квадрат 3 дюйма.
    - Обязательно отметьте по два места для каждого края, чтобы убедитесь, что вы делаете точный разрез.
    - Не используйте карандаш для пометок на картоне; Используйте Exacto лезвие, которое производит более точную отметку.
  4. Сделайте три надреза в этом квадрате, чтобы получилось чистый стык на краю куба.
    - Подумайте, с какой стороны картона вы хотите лицевой стороной наружу.
    - От каждого выбранного края отмерьте 1/8 дюйма и слегка отметьте с помощью лезвия Exacto.
    - Замените лезвие Exacto.
    - Удалите первые два слоя с каждого из трех краев. Сделайте несколько легких движений ножом, пока третий слой – неразрезанный.
    - Не обрезайте полностью через три слоя картон. Вам нужно оставить бумагу, чтобы она закройте необработанный край лица, который к нему присоединяется.
  5. Снимите два слоя картона с трех краев.
2. Повторите эти шаги еще три раза, чтобы сделать четыре стороны куб. В частности, повторяйте этап смены лезвия каждый раз. раз вы начнете новую сторону.
3. Сделайте верхнюю и нижнюю грани
  1. Замените лезвие Exacto.
  2. На свежем краю листа картона вырежьте 3 дюйма квадрат из картона для вершины вашего идеального куба.
  3. Повторите то же самое для нижней грани.
4. Протестируйте сборку куба.
  1. Соберите стороны так, чтобы у вас была полочка сверху и нижние грани, поэтому необработанные края все покрыты.
5. Склейте кубики.
  1. Сделайте тестовую сборку без клея, чтобы убедиться, что вы знаете, как ваш куб идет вместе.
  2. Возьмите кусок картона (он же клейкую подушечку) и положите капля клея на нем.
  3. С помощью небольшой палочки или пальца перенесите клей с блокнот к вашей части.
  4. Нанесите тонкий слой клея на бумажную часть сустав. (На гофрированную часть не надевать – он капля и не прилипает.) Убедитесь, что у вас есть только тонкий слой клея и следите за тем, чтобы клей был только на стыке, а не на всех над вашим кубом.
  5. Удерживайте стык вместе примерно 10 секунд перед переход к следующему стыку.
  6. Большинство людей считают, что проще всего собрать стороны вокруг низ и добавить верх в качестве последнего шага.
Подпишите свой куб!

Советы по стрижке

Будьте осторожны и обращайте внимание – как на свои конечности, так и на те из людей вокруг вас.
Положите линейку пробковой стороной вниз.
Дважды проверьте, что вы режете доску.
Порез на себя. Режьте медленно и осторожно.
Некоторым людям легче резать стоя, потому что угол и давление лучше.

Будьте осторожны, чтобы не порезать столы и не нанести на них клей

[email protected]

Сколько квадратов? | Квадрат и кубики | CBSE | Класс 5

Каждый прямоугольник состоит из 12 равных квадратов, поэтому все они имеют одинаковую площадь, но длина границы будет разной.

Какой из этих прямоугольников имеет самый длинный периметр?
Какой из этих прямоугольников имеет наименьший периметр?

От детей не требуется, чтобы они выучили определение термина «область», но они разовьют понимание этого понятия с помощью подходящих примеров.Дайте им много возможностей в классе сравнивать предметы по площади и угадывать, что больше. Можно сравнить такие вещи, как печати, листья, следы, стены в классе и т. Д.

Марки меры

Посмотри на эти интересные марки

Сколько квадратов со стороной в один сантиметр покрывает штамп А?
А штамп Б?
Какая марка имеет самую большую площадь?
Сколько квадратов со стороной 1 см покрывает эта марка?
Сколько стоит самая большая марка? квадратные см.
Какие две марки имеют одинаковую площадь?
Сколько стоит каждая из этих марок? квадратные см.
Площадь наименьшего штампа – см кв.
Разница между площадью самого маленького и самого большого штампа составляет квадратный сантиметр. .

Соберите несколько старых марок. Разместите их на квадратной сетке и найдите их площадь и периметр.

Угадать

У кого больше площадь – у одного из ваших следов или страницы этой книги?
Какая из них имеет меньшую площадь – две банкноты по пять рупий вместе или банкнота в сто рупий?
Посмотрите на банкноту в 10 рупий.Его площадь больше ста квадратных сантиметров?
Площадь синей фигуры больше площади желтой фигуры? Почему?
Периметр желтой фигуры больше периметра синей фигуры? Почему?

Насколько велика моя рука?

Проведите рукой по квадратному листу на следующей странице.

Как вы решите, чья рука больше – ваша рука или рука вашего друга?

Какая у тебя площадь руки? _______ квадратных см.

Какова площадь руки вашего друга? _______ квадратных см.

Мои следы

Чей след больше – твой или твой друг?
Как вы решите? Обсудить
Площадь ваших следов одинакова?
Угадайте, след какого животного будет иметь такую же площадь, что и ваш. Обсуждать.
Вот следы животных в натуральную величину.Угадай площадь их следов

На этом этапе детям не нужно считать каждый квадрат. Поощряйте их определять самые большие квадраты и прямоугольники в пределах следа, чтобы знать их площадь, а затем подсчитывать маленькие квадраты неправильной формы. Хотя область прямоугольника будет описана в главе 11, некоторые дети могут обнаружить, что они могут найти эту область быстрее посредством умножения.

Сколько во мне квадратов?

В этом упражнении дети должны заметить геометрическую симметрию фигур, чтобы определить свою область.Поощряйте детей разрабатывать собственные стратегии. В этих примерах округление не требуется.

Попробуйте треугольники

Помогите Садику найти еще несколько таких треугольников. Нарисуйте еще как минимум 5.

Завершите форму

Суручи нарисовал две стороны фигуры. Она попросила Асифа дополнить фигуру еще двумя сторонами, чтобы ее площадь составила 10 квадратных сантиметров.

Он прав? Обсуждать.
Объясните, что зеленая область составляет 4 см2, а желтая область – 6 см2.
Суручи прав? Сколько стоит синяя область? Объяснять.
Можете ли вы придумать другие способы завершения фигуры?
Попробуйте другие способы самостоятельно.
Теперь попросите своих друзей решить их.

Время практики

Это одна из сторон фигуры. Завершите форму так, чтобы ее площадь составляла 4 см кв.
Здесь нарисованы две стороны фигуры. Завершите форму, нарисовав еще две стороны, чтобы ее площадь была меньше 2 квадратных сантиметров.

Детей можно посоветовать создавать фигуры с прямыми или изогнутыми краями, чтобы покрыть заданную область. Это упражнение можно расширить, попросив детей нарисовать на бумаге в квадрате столько фигур, сколько они могут на данной площади, и угадать самый большой или самый маленький периметр.Их также можно попросить проверить свои догадки, измерив размеры фигур. В случае изогнутых краев для измерения периметра можно использовать резьбу.

Вот прямоугольник площадью 20 кв.
1. Нарисуйте одну прямую линию в этом прямоугольнике, чтобы разделить его на два равных треугольника. Какова площадь каждого из треугольников?
2. Нарисуйте одну прямую линию в этом прямоугольнике, чтобы разделить его на два равных прямоугольника.Какова площадь каждого из меньших прямоугольников?
3. Нарисуйте в этом прямоугольнике две прямые линии, чтобы разделить его на один прямоугольник и два равных треугольника.
- Какова площадь прямоугольника?
- Какова площадь каждого из треугольников?

Пазлы с пятью квадратами

Измерьте сторону небольшого квадрата на квадратной бумаге, показанной ниже. Сделайте столько формы по возможности используя 5 таких квадратов.Для вас нарисованы три.

Сколько разных фигур вы можете нарисовать? ___________
Какая форма имеет самый длинный периметр? Сколько? _______ см
Какая форма имеет самый короткий периметр? Сколько? _______ см
Какова площадь фигур? _______ квадратных см. Все просто!

Вы получили все 12 фигур из 5 квадратов?

Нарисуйте все 12 фигур на листе картона и вырежьте их.

Попробуйте расположить ваши 12 фигур другим способом, чтобы получился прямоугольник 10 * 6. Вы могли бы это сделать?

Попробуйте еще одну головоломку

Из этих 12 фигур нужно создать прямоугольник 5 * 12. Для этого существует более 1000 способов. Если вы можете найти хотя бы один, это здорово!

Игровое время

Вот шахматная доска. Играйте в эту игру со своим партнером, используя один набор из 12 фигур.

Первый игрок выбирает одну фигуру из набора и кладет ее на доску, покрывающую любые пять квадратов.

Другой игрок выбирает другую фигуру и кладет ее на доску, но она не должна перекрывать первую фигуру.

Продолжайте по очереди, пока один из вас не перестанет идти дальше.

Выигрывает тот, кто поставит последнюю фигуру!

Сделайте свою плитку

Вспомните образцы пола из книги 4 по математике и магии (страницы 117-119). Вам нужно было выбрать правильную плитку, которую можно было повторить, чтобы создать узор, чтобы не оставалось зазоров.

Поощряйте детей попытаться решить эти головоломки «пентамино» дома.Такие упражнения могут быть разработаны для фигур с 6 квадратами (гексомино), и в этом случае будет возможно 35 различных форм.

Зири пошел в магазин и был удивлен, увидев разный узор плитки на полу.
Разве это не красиво!

Можете ли вы найти плитку, из которой повторяется каждый из этих рисунков пола?
Обведите по плитке в каждом узоре.

Посмотрев на узоры, Зири захотела сделать свою собственную желтую плитку.Вы тоже таким способом делаете плитку.

Шаг 1: Возьмите кусок картона или плотной бумаги. Нарисуйте на нем квадрат со стороной 3 см. Шаг 2: нарисуйте треугольник на любой из сторон этого квадрата. Шаг 3: Нарисуйте еще один треугольник того же размера на другой стороне квадрата. Но на этот раз нарисуйте его внутри квадрата. Шаг 4: Вырежьте эту фигуру из картона. Ваша плитка готова! Что это за площадь?

Сделайте узор из плитки.Обведите фигуру, чтобы она повторилась на странице, но помните, что между ними не должно быть промежутков.

Зири сделала узор из своих желтых плиток (вы знаете площадь ее плитки).

Ответь на эти —

Сколько плиток она использовала?
Какова площадь рисунка пола, созданного Зири?

Время практики

Зири пытался сделать другие плитки. Она начала с квадрата со стороной 2 см и сделала такие формы.
Посмотрите внимательно на них и узнайте:

Какой из этих форм украсит пол (без зазоров)? Обсуждать. Какова площадь этих фигур?
Создайте дизайн на своей копии, выложив эти фигуры плиткой.
Теперь вы создаете свои собственные новые плитки из квадрата. Можете ли вы сделать то же самое с треугольником? Попробуй сделать это.

В классах III и IV основные формы, такие как квадраты, прямоугольники, шестиугольники, треугольники, круги и т. Д., Использовались для проверки того, какие из них можно облицовывать, а какие нет, для создания рисунков пола.Теперь дети должны иметь возможность изменять основные формы для создания различных форм мозаики.